Maßvorsätze umwandeln

Eselsbrücken

Erklärt mit Kommaverschiebung:

graph LR A["Maßvorsatz"] -- wird größer --> B["Komma nach ⇽"] A -- wird kleiner --> C["Komma nach ⇾"] B -- Beispiel --> D{{"5000,0mV ⇽ 5,0V ⇽ 0,005kV"}} C -- Beispiel --> E{{"0,005kV ⇾ 5,0V ⇾ 5000,0mV"}}

Erklärt mit Multiplikation und Division

graph LR A["Maßvorsatz"] -- wird größer --> B["dividieren"] A -- wird kleiner --> C["multiplizieren"] B -- Beispiel --> D{{"5000mV : 1000 = 5V; 5V : 1000 = 0,005kV"}} C -- Beispiel --> E{{"0,005kV * 1000 = 5V; 5V * 1000 = 5000mV"}}

manch einem hilft diese Verdeutlichung

graph LR A["Giga (G)"] -->|* 1000| B("Mega (M)") B -->|: 1000| A B -->|*1000| C{"Kilo (k)"} C -->|: 1000| B C -->|*1000| D{"1"} D -->|: 1000| C

graph LR D{1} -->|*1000| E{"milli (m)"} E -->|: 1000| D E -->|*1000| F{"mikro (µ)"} F -->|: 1000| E F -->|*1000| G{"nano (n)"} G -->|: 1000| F

bei Längenmaßen gibt es noch centi und dezi als Maßvorsatz

graph LR D{1} -->|*10| E{"deci (d)"} E -->|: 10| D E -->|*10| F{"centi (c)"} F -->|: 10| E

Beispiel 1

10,5 mW sind umzuwandeln in kW

Mit Kommaverschiebung

Die Maßeinheit wird größer => Komma nach links (⇽)

Von milli nach normal => 3 Stellen nach links verrücken:

\(10,5\ mV =0,0105\ V\)

von normal nach kilo => Komma 3 Stellen nach links verrücken:

\(0,0105\ V = 0,000 010 5\ kV\)

Insgesamt ist das Komma 6 Stellen nach links gewandert und das Ergebnis ist:

\(0,0000105\ kV\)

Mit Multiplikation / Division

Die Maßeinheit wird größer => es wird dividiert

von milli nach normal => Division durch 1000:

\(10,5\ mV : 1000 = 0,0105\ V\)

von normal nach kilo => Division durch 1000:

\(0,0105\ V : 1000 = 0,0000105\ kV\)

Insgesamt wäre es also:

\(10,5\ mV : 1000 : 1000 = 10,5\ mV : 1000 000 = 0,0000105\ kV\)

Beispiel 2

Wieviel Watt sind 0,5430223 GW?

Mit Kommaverschiebung

Die Maßeinheit wird kleiner => Komma nach rechts (⇾)

von giga zu mega => 3 Stellen nach rechts verrücken:

\(0,5430223\ GW=543,0223\ MW\)

von mega zu kilo => 3 Stellen nach rechts verrücken:

\(543,0223\ MW = 543022,3\ kW\)

von kilo zu normal => 3 Stellen nach rechts verrücken:

\(543022,3\ kW = 543022300\ W\)

Insgesamt wurde das Komma 9 Stellen nach rechts verschoben.

Mit Multiplikation / Division

Die Maßeinheit wird kleiner => es wird multipliziert

von giga nach mega => Multiplikation mit 1000:

\(0,5430223\ GW \cdot 1000 = 543,0223\ MW\)

von mega nach kilo => Multiplikation mit 1000:

\(543,0223\ MW \cdot 1000 = 543022,3\ kW\)

von kilo nach normal => Multiplikation mit 1000:

\(543022,3\ kW \cdot 1000 =543022300\ W\)

insgesamt wäre es also

\(0,5430223\ GW \cdot 1000\cdot 1000\cdot 1000=0,5430223\ GW\cdot 10^9=543022300\ W\)

Was bedeutet nun das \(\cdot 10^9\)?

In der Kommaverschiebung mußten wir bei Beispiel zwei das Komma um 9 Stellen verschieben. Die 9 Stellen entsprechen dem Exponenten in \(10^9\). Somit gilt
\(\cdot 10^9 \Rightarrow \mathrm{Komma\ 9\ Stellen\ nach\ links}\)

Wie wäre es bei \(:10^9\)?

\(:10^9\Rightarrow\mathrm{Komma\ 9\ Stellen\ nach\ rechts}\)

Zusammengefaßt in ein Flussdiagramm

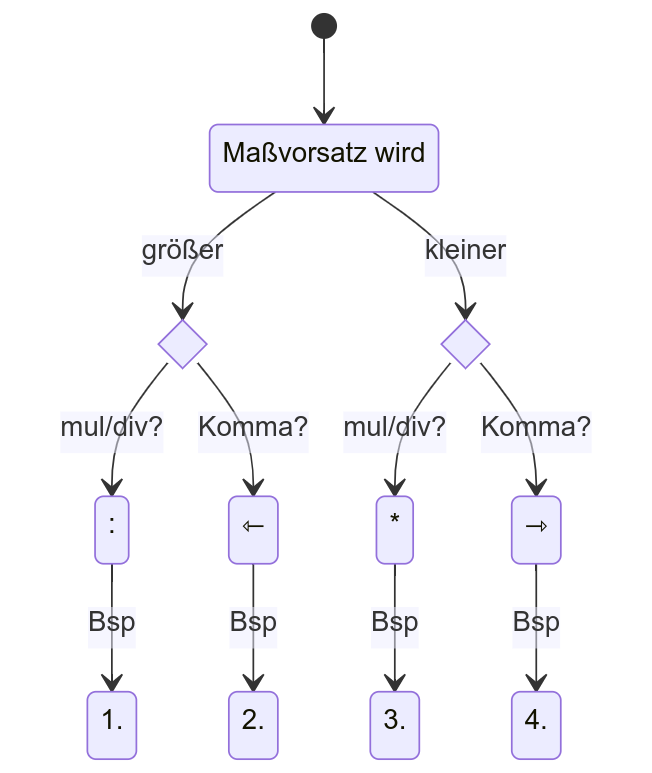
Beispiele 1. - 4.:
1. \(5000\ mW : 1000 =5\ W\)
2. \(5000,0\ mW \leftarrow 5\ W\)
3. \(5W \cdot 1000 = 5000\ mW\)
4. \(5,0\ W \rightarrow 5000,0\ W\)

Backlinks

01 - Maßvorsätze verwenden
2022-10-20